stocksklion.blogg.se - Quadratic graph

QUADRATIC GRAPH HOW TO
QUADRATIC GRAPH SERIES

QUADRATIC GRAPH HOW TO

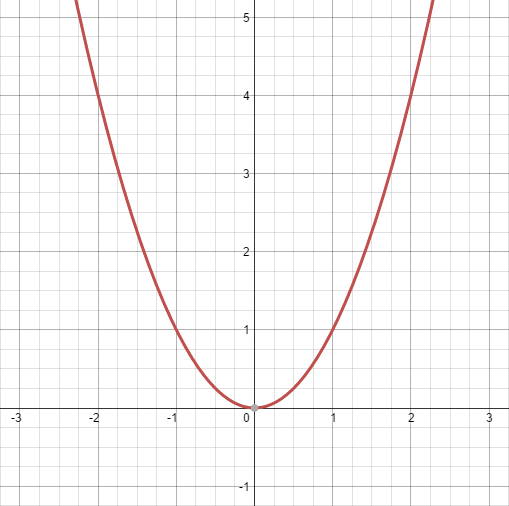
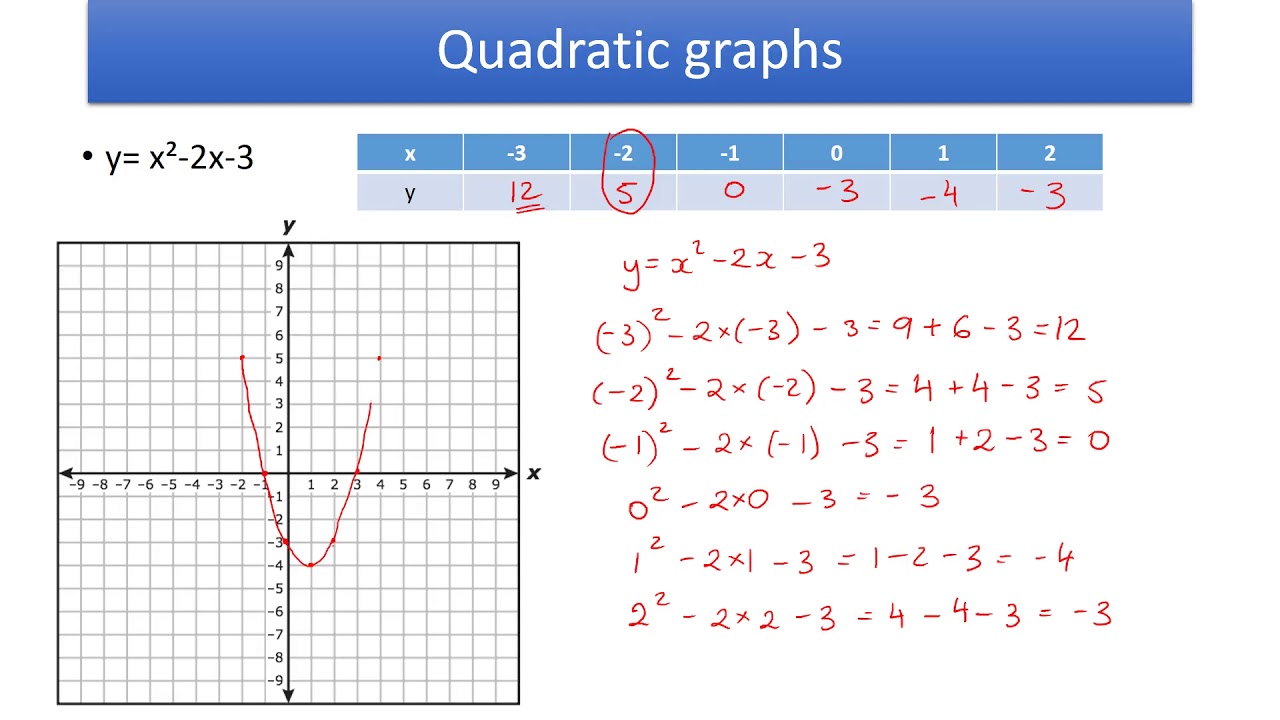
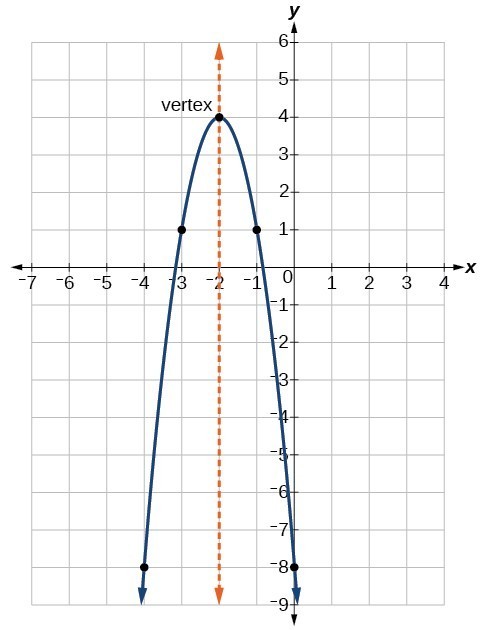
How to Do Graphing Quadratic Functions In Standard Form?įor graphing quadratic functions using the standard form of the function, we can either convert the general form to the vertex form and then plot the graph of the quadratic function, or determine the axis of symmetry and y-intercept of the graph and plot it. Then, substitute this value of x in the quadratic function f(x) = ax 2 + bx + c to determine the y-coordinate of the vertex. To determine the vertex of the parabola when graphing quadratic equations, we determine the x-coordinate of the vertex using the formula x = -b/2a. How to Find the Vertex when Graphing Quadratic Functions? The final vertex of the parabola will be at (-b/2a, -D/4a). The direction of the shift will be decided by the sign of D/4a. Step 3: a(x + b/2a) 2 to a(x + b/2a) 2 - D/4a: This transformation is a vertical shift of magnitude |D/4a| units.

The new vertex of the parabola will be at (-b/2a,0). The direction of the shift will be decided by the sign of b/2a.

Step 2: ax 2 to a(x + b/2a) 2: This is a horizontal shift of magnitude |b/2a| units.

Graphing quadratic functions is a technique to study the nature of the quadratic functions graphically. Graphing quadratic functions is a process of plotting quadratic functions in a coordinate plane. Related Topics on Graphing Quadratic FunctionsįAQs on Graphing Quadratic Functions What is Graphing Quadratic Functions?

Graphing Quadratic Functions can be done using both general form and vertex form.

The coefficient a in f(x) = a(x - h) 2 + k determines whether the graph of a quadratic function will open upwards or downwards.

The graph of the quadratic function is in the form of a parabola.

Important Notes on Graphing Quadratic Functions Using all this information, we can plot the graph of the quadratic function f(x) = 2x 2 + 4x + 4. Now, we will determine the y-intercept of the parabola which is given by (0, c) = (0, 4). Hence, x = -1 is the axis of symmetry for the graph of f(x) = 2x 2 + 4x + 4 and the vertex of the graph also has x-coordinate equal to -1. Next, for graphing quadratic function f(x) = 2x 2 + 4x + 4, we determine the axis of symmetry of the parabola which is given by, x = -b/2a = -4/(2.2) = -1. A larger and positive 'a' makes the function increase faster and the graph appear thinner. The coefficient a also controls the speed of increase (or decrease) of the graph of the quadratic function from the vertex. The coefficient a = 2 > 0, implies the graph of the quadratic function will open upwards. Now, for graphing quadratic functions using the standard form of the function, we can either convert the general form to the vertex form and then plot the graph of the quadratic function, or determine the axis of symmetry and y-intercept of the graph and plot it.įor example, we have a quadratic function f(x) = 2x 2 + 4x + 4. The general equation of a quadratic function is f(x) = ax 2 + bx + c.

Graphing Quadratic Functions in Standard Form The graph of quadratic functions can also be obtained using the graphing quadratic functions calculator. The following figure shows an example shift: The magnitude of the scaling depends upon the magnitude of a. If a is negative, the parabola will also flip its mouth from the positive to the negative side. Step 1: x 2 to ax 2: This will imply a vertical scaling of the original parabola.

QUADRATIC GRAPH SERIES

Now, to plot the graph of f(x), we start by taking the graph of x 2, and applying a series of transformations to it: Here, the vertex of the parabola is (h, k) = (-b/2a, -D/4a). The term D is the discriminant, given by D = b 2 - 4ac. First, we rearrange it (by the method of completion of squares) to the following form: f(x) = a(x + b/2a) 2 - D/4a. Consider the general quadratic function f(x) = ax 2 + bx + c. We will study a step-by-step procedure to plot the graph of any quadratic function. Graphing Quadratic Functions in Vertex Form